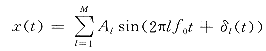|
电力系统频率测量综述
返回
谢小荣 韩英铎
摘 要 较 为全面地综述了国内外在电力系统频率概念及其测量技术方面的研究成果。以观测模型为依据,探讨了各种电力系统频率概念的异同;针对频率测量的目的,提出测 量的基本要求;以测频主算法的数值特征为线索对历史上各种测量算法进行了系统的分类与评述;讨论了测量的硬件实现及其测试;最后对电力系统频率测量的发展 趋势提出看法。
关键词 电力系统频率(偏移) 信号观测模型 频率测量算法
分类号 TM 764
AN OVERVIEW ON POWER SYSTEM
FREQUENCY MEASUREMENT
Xie Xiaorong, Han Yingduo(Tsinghua University, 100084, Beijing,
China)
Abstract The recent achievements in the field of power
system frequency measurement are summarised in this paper. Firstly, the
various definitions of power system frequency are described on the basis of
signal observation model. Secondly, some basic requirements of frequency
measurement are put forward in the light of application purpose. Then comes
the classification and assessment of the multifarious frequency estimation
algorithms. The hardware realization and test are also touched on. In
conclusion, the trend of power system frequency measurement is naturally
educed.
Keywords power system frequency (deviation) signal observation model frequency measurement algorithm
0 引言
“频 率”概念源于针对周期性变化的事物的经典物理学定义,由于电力系统中许多物理变量具有(准)周期性特征,故这一概念在电业技术中得到广泛的应用。电力系统 频率一方面作为衡量电能质量的指标,需加以动态监测;另一方面作为实施安全稳定控制的重要状态反馈量,要求能实时重构。因此,频率测量成为电力系统运行控 制的重要技术。
随着大容量、超高压、分布式、异构型复杂电力网络的形成和人们对其行为特性的深入理解,基于传统的纯恒幅正、余弦信号基础上定义的电力系统频率概念及其测量技术在解决现代电网诸多问题时遇到了巨大的挑战:
a.无论在稳态还是暂态过程中,所描述物理量(电压、电流等)的非严格周期性,即信号频谱由离散谱进入连续谱;
b.现代电力系统本身存在许多随机性因素,测量也不可避免地受到各种噪声的干扰,文献[1]称电力系统的频率偏移是具有高斯分布的随机参数,即具有不确定性;
c.时空分布性,即频率不能作为系统单一的状态变量[2];
d.多相系统的不对称性,影响因素的复杂性等。
总之,大网络系统所固有的非线性、随机性、分布性、非平稳性和影响因素的复杂性等特征,难以用传统的频率概念加以准确描述。许多学者深入地探讨了上述问题,对电力系统频率概念及其测量技术进行了广泛的研究。
本文在已有研究成果的基础上,以信号观测模型为线索认识总结了电力系统频率概念的各类定义,并对众多的测量算法进行了分类说明,从而为进一步开展电力系统频率的理论研究和工程应用打下基础。
1 信号观测模型和电力系统频率概念
信号观测模型就是对电力系统频率概念及其测量技术所 基于的物理信号的数学描述。电力系统频率概念的引申或扩展,关键在于信号对象x(t)的选取及其观测模型的确立。信号观测模型的复杂化过程集中体现了这一 领域的不断发展:从简单的纯恒幅正、余弦信号,到周期和非周期信号的傅里叶分解,进而引入信号动态,直至分布式随机模型的应用。
常见信号观测模型及频率概念定义如下。
a.基于纯恒幅正、余弦信号的传统频率概念:
x(t)=Amsin(2πft+θ)
(1)
或
x(t)=Am sin(2πf0t+δ(t))
定义
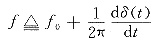
(2)
其中 x(t)普遍取单一的相(线)电压或相电流。
b.考虑有限整次谐波污染,在傅里叶分解模式下:
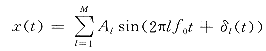
(3)
定义基波频率
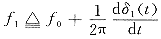
c.进一步考虑衰减直流分量影响,在观测模型下:
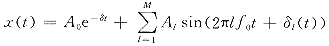
(4)
如前定义基波频率f1。
d.在前述信号观测模型基础上附加简单的噪声分量,如:
x(t)=Am sin(2πft+θ)+ξ(t)
(5)
x(t)=Am sin(2πf0t+δ(t))+ξ(t)
(6)
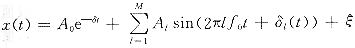
(7)
其中 ξ(t)代表噪声等非特征分量,可作类似定义。
e.近期较多文献将经典的周期导出频率定义扩展到特定相(向)量瞬时旋转速度意义下的瞬时频率(instantaneous
frequency)概念。定义电压空间向量:
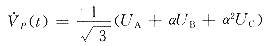
(8)
其中 α=ej2π/3。
进而定义
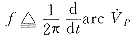
(9)
进一步考虑分布性和随机性特征,在地区频率
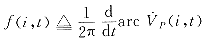
(10)
基础上定义系统频率概念:
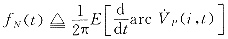
(11)
并在分段各态遍历假设下,系统频率对样本期望的定义可通过特定样本对时间的期望来求取。
与频率测量密切相关的另一个概念是频率偏移(frequency
deviation),即Δff-f0,其中f0为系统额定频率。
电力系统真实物理信号的动态非常复杂,特别是在系统运行方式跳变(如故障、操作、控制装置动作等)及其后续过渡过程中,信号的变化远非上述观测模型可以 精确描述。但是,一方面由于目前人们对电力系统认识水平及其解析工具的历史限制以及基于此而产生的对频率概念应用范围的要求;另一方面可以通过各种措施 (如信号处理技术)将真实信号改造成具有接近模型描述的形式,使得上述观测模型及其频率概念在不同程度上揭示了电力系统某方面真实的物理本质,能用于描述 系统的动态特征和实施安全稳定控制。随着电力系统自身及其相关学科的发展,“电力系统频率”的概念也会不断演化。
2 电力系统频率测量释义及其基本要求
电力系统频率测量的实质 是信号观测模型的动态参数辨识问题,即利用真实系统物理信号输入,通过一定的信号处理和数值分析过程,实现对预定模型参数的较好估计。从操作对象来看,主 要是数字信号处理问题;从测量目标来看,是灰箱辨识问题;而从实现测量所借助的工具来看,是数值算法(软件)和它借以实现的各种模拟、数字装置(硬件)的 设计问题。由于对频率的理解和应用的实际要求不同,频率测量在上述各个方面存在较大差异,虽然其实现策略不一样,但仍有一些共同的基本要求:
a.反映电力系统的物理真实性和实施控制的有效性。即不会由于模型和算法的差异而导致脱离电力系统真实物理本质的测量结果,且基于实时频率估计的控制作用应是正确而可靠的。
b.精度要求。即达到减少误差、精确测量的目的,这取决于观测模型与真实信号的符合程度、数值算法及硬件实现等多方面因素,一般以对抗噪声、谐波、衰减直流等非特征信号分量的能力来衡量。
c.速度要求。要求具有较快的动态跟踪能力,测量时滞小。
d.鲁棒性。在电力系统的正常、异常运行乃至故障条件下,均能可靠响应。
e.实现代价小。这一要求往往与上述要求相冲突,在实践中应酌情考虑,在达到应用要求的前提下,力求较高的性能价格比。
3 电力系统频率测量算法
测频算法设计是频率测量的核心环节,也是各文献着重论述和相互区别之所在。一般而言,频率测量包括3个步骤:信号预处理;频率(偏移)测量;结果再处理。其中信号预处理和结果再处理是辅助算法,为频率(偏移)测量服务,以优化测量性能,达到实际应用的目的。
频率(偏移)测量虽然在算法设计和实现中占据主导地位,但辅助算法在很大程度上决定了其能否预期执行和装置的可靠性,故不能忽视对它的设计。实践表明, 获得一个时滞小、去噪能力强,同时又能为后续控制分析提供高精度频率特征的辅助算法并不容易。辅助算法的选择主要决定于以下因素:
a.输入信号的动态与主算法所基于的观测模型的符合程度,以及后续控制或分析所需的频率特征(频率偏移还是频率振荡);
b.主算法的数值行为;
c.给定应用的时间响应和精度要求;
d.软硬件实现约束。
以下对各文献提出的测频算法的总结分类以频率(偏移)测量所基于的数值原理为标准,附带论及其相应的辅助算法。
3.1 周期法
原始的周期法(或称零交法:zero-crossing
algorithm)基于第1节论及的简单信号观测模型a,通过测量信号波形相继过零点间的时间宽度来计算频率。该方法物理概念清晰、易于实现,但精度 低,受谐波、噪声和非周期分量的影响,实时性不好,因此,实用的测频装置很少单一地应用原始周期算法。对它的改进主要是提高其测量精度和实时性,典型的改 进算法有水平交(level crossing)算法[3]、高次修正函数法[4]和最小二乘多项式曲线拟合法[5],它们以计算量和复杂度为代价来提高算法的精度和响应速度(原始周期算法的时延决定于信号特征而非计算量),一定程度上丧失了原有的零交算法的简明性。
3.2 解析法[6,7]
对信号观测模型进行数学变换,将待测量f或Δf表示为样本值的显函数来估计。解析法测频的特点是:涉及复杂的数学推导,为简化分析和计算,只能采用简单 的信号观测模型,难以考虑谐波、非周期分量和噪声影响;算法简明,计算量不大,较传统的周期法有所改进,但难以适应非稳态频率的测量,即使在稳态条件下, 也必须有严格的前置滤波环节,且算法推导有近似化过程,精度总体不高。该方法可应用于速度和精度要求不高且信号的非特征分量可以忽略的场合。
3.3 误差最小化原理类算法
采用含噪声的信号观测模型,算法设计以最小化误差的某种范数为目标,由于数学分析和信号处理领域对此类算法有详细的阐述,故问题的关键在于将测量求解化为相应的标准格式,并减少计算量。
3.3.1 最小二乘算法
应用最小二乘算法(least error
square algorithm,缩写为LES)[8~11]检测频率的基本原理是在最小方差意义下实现样本数据与模型的最佳拟合,即对量测矩阵方程Z=H(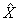 )+V,在极小化误差向量加权二次范数min[J( )+V,在极小化误差向量加权二次范数min[J(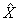 )=VTθV]的约束下利用观测值求解待测量,为简化分析计算,一般采用线性量测矩阵方程,且取加权矩阵θ为单位矩阵。 )=VTθV]的约束下利用观测值求解待测量,为简化分析计算,一般采用线性量测矩阵方程,且取加权矩阵θ为单位矩阵。
一般而言,LES算法对随机噪声的抑制能力强,而对抗谐波、衰减直流等非特征信号分量的能力与所采用的信号观测模型和辅助算法有关。文[8,11]在构造线性量测矩阵时采用泰勒级数截断的方法限制了其测量精度和范围;用查找表(look-up-table)来减小误差[9]以 适应因较大范围频率测量的方法本质上对噪声有放大作用,而使估计的波动性增大的情况。文[11]的自校正算法有利于改善计算精度和扩大测量范围,但计算量 大增,算法收敛慢,应用于离线谐波检测尚可。文[10]基于第1节论及的观测模型b构造线性量测矩阵,通过初值预定的递推最小二乘法估计二维状态向量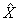 ,进而计算Δf,但计算对噪声有放大作用;采用自适应调整采样率方案提高了精度和跟踪范围,但又带来了计算量剧增、时滞大等缺陷,且算法敏感于初值。 ,进而计算Δf,但计算对噪声有放大作用;采用自适应调整采样率方案提高了精度和跟踪范围,但又带来了计算量剧增、时滞大等缺陷,且算法敏感于初值。
3.3.2 最小绝对值近似
最小绝对值近似(least
absolute value approximation,缩写为LAV)方法与LES算法不同之处在于,它以极小化误差向量的一次范数,即min[J(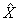 )=‖V‖1]为求解约束条件。文[12]提出采用二步LES法或LP(线性规划)法求解 )=‖V‖1]为求解约束条件。文[12]提出采用二步LES法或LP(线性规划)法求解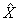 的数值方法。LAV算法较LES算法在采样率、数据窗长度位置及坏数据对测量精度的影响等方面有所改善,但计算量大得多。 的数值方法。LAV算法较LES算法在采样率、数据窗长度位置及坏数据对测量精度的影响等方面有所改善,但计算量大得多。
3.3.3 牛顿类算法[13,14]
牛顿类算法(Newton-type algorithm)基本原理是将牛顿类迭代算法和最小二乘原理结合起来求解超定非线性方程组。该算法计算复杂,在待估高次谐波分量较多时,工作量十分可 观;且算法参数设置不恰当时,极易出现数值不稳定现象;迭代初值选择困难,文献[13]提出的用内置LES或傅里叶滤波法来提供初值的方法代价太大;精度 受问题规模制约;数据窗长度为0.02 s。算法优点是能测量系统谐波。因此,该算法难以适用于实时频率测量或控制,对于离线谐波分析也许有一定价值。
3.3.4 离散(扩展)卡尔曼滤波算法
离散(扩展)卡尔曼滤波法(discrete
[extended] Kalman filter algorithm,缩写为D[E]KF)是一种高效优化的信息处理方法,它对离散随机动态过程及其含噪声量测变换:
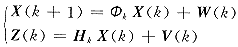 (线性KF) (线性KF)
或
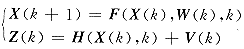 (非线性KF) (非线性KF)
在min[E‖X(k+1)-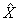 (k+1)‖22]的原则下递推估计状态向量 (k+1)‖22]的原则下递推估计状态向量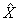 (k+1)。将卡尔曼滤波算法应用于电力系统频率测量的关键是模型的建立(动态方程、量测方程和随机序列的统计特性Qk,Rk)和状态变量、协方差阵初值( (k+1)。将卡尔曼滤波算法应用于电力系统频率测量的关键是模型的建立(动态方程、量测方程和随机序列的统计特性Qk,Rk)和状态变量、协方差阵初值(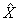 0,P-0)的正确估计。 0,P-0)的正确估计。
卡尔曼滤波、递归最小二乘(recursive
least-square,缩写为RLS)算法和LMS(least mean-square)算法(一种应用随机梯度算法的自适应FIR滤波)对于线性、高斯分布零均值噪声的动态过程是无偏最小方差的有效估计;但应用于频 率测量时,由于部分线性近似和噪声模型的简化,估计一般是有偏的。文献[15~17]基于的信号观测模型都比较简单,特别是文献[15]认为信号动态是确 定性的,又采用恒定的噪声协方差阵,估计精度总体不高,跟踪范围窄(±2 Hz);文献[16]采用两阶段自适应(E)KF算法,提高了抗干扰能力和精度,估计结果平滑性好,但计算量比文献[15]算法大得多,动态跟踪能力受到 限制,收敛速度接近0.2 s;文献[17]算法与文献[16]算法性能相似,都采用自适应策略和后继平滑过程,不同之处是用时变遗忘(或自适应)因子序列{λ(k)}实时估计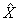 k, k,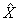 k,并对主算法输出进行移动平均(moving-average,缩写为MA)滤波(即全零点滤波)处理以获得平滑结果。 k,并对主算法输出进行移动平均(moving-average,缩写为MA)滤波(即全零点滤波)处理以获得平滑结果。
误差最小化原理类算法的最大优点是能较好地抑制具有白噪声动态的干扰信号,由于算法中有复杂的数学运算,它要借助于软件编程实现,随着数字信号处理硬件的发展,该类算法逐渐从原来的离线分析应用进入实时控制领域。
3.4 DFT(FFT)类算法及其改进
DFT(FFT)是一种典型的数字滤波技术,对于第1节论及的观测模型d(假设δ=0),在采样率和数据窗选择合适的情况下,滤波算法能正确求出模型参数;考虑到真实测量偏离理想条件,利用前后窗DFT(FFT)结果估计系统的基频。
DFT(FFT)算法具有内在的不敏感于谐波分量的特性,但对信号的周期延拓引入频率混叠,实际应用中需要精细设计前置抗混叠滤波。利用DFT(FFT)过程求取模型参数进而计算频率偏移的方法[18]过 于简单粗糙,不实用;文献[5]提出了基于最小二乘意义下的多项式拟合的改进算法,可以提高测量精度,但计算量增加,时滞增大,且带来了LES算法的易数 值病态化问题。文献[19,20]利用FFT算法在频率偏移工频时固定抽样频率导致的泄漏效应来估计系统频率,其中后者采取递推FFT法以减少计算量;该 方法测量范围窄(大约为额定频率的±10%),且敏感于噪声和信号幅值变化;对它的改进包括自适应调整采样间隔[21,22]和自适应调整数据窗长度[23],前者的优点是提高了测量范围、精度和算法稳定性,后者的定点采样方法易于硬件实现。
3.5 正交去调制法
正交去调制法(quadrature demodulation algorithm,缩写为QD)将采集到的信号x(t)乘以一个去调制复载波e-j2πfdt,得到x′(t)=x(t)*e-j2πfdt,在信号x′(t)的基础上测量原信号的频率。根据fd在测量过程中是否动态地改变分为固定频率去调制[5,24~27]和变频去调制[28]。由于x′(t)包含了丰富的谐波分量和噪声,故一般需要精细的滤波技术。去调制技术与DFT(FFT)在本质上有异曲同工之妙。
去调制技术测频一般动态跟踪能力较好,且比较容易通过滤波去除高频噪声和谐波干扰,但不易对付工频附近的噪声,固定频率去调制若不附加补偿措施,则精度 不高,测量范围狭窄(如文献[5]算法)。文[26]算法采用对三相电压进行αβ变换所得空间电压相量为观测模型,优点是在负序分量较少时,无需滤除倍频 分量,但对其他谐波和噪声无特殊去除效果,当负序分量较大时(不对称故障),同样引入倍频成分。文[24]用正、余弦正交FIR滤波器实现去调制,并采用 了最优预测算法动态补偿不匹配误差以提高测量精度和算法稳定性。文献[25]对文献[24]算法在滤波器精确设计、对抗冲击频率动态和输出平滑等方面的问 题进行了深入的理论分析,并提出相应的对策,但过多地引入滤波器带来较大的时滞,影响动态性能。文献[28]使用锁相环(PLL)动态跟踪频率变化以实现 变频率去调制,算法具有较好的动态响应和针对非工频分量的鲁棒性,但有冲击频率动态问题。文献[27]的固定频率去调制算法用一个自适应滤波器去除引入的 倍频分量。
去调制测频算法的快速响应特性使得它在基于频率(偏移)动态的实时控制系统中得到广泛应用,但精细的滤波技术和避免冲击频率动态干扰是应用这一算法的前提。
其他算法如谱分析法[21,27,29]、二次型商法[30]、虚拟转子法[31]、正交信号法(典型的如90° Hilbert滤波算法)和最大似然法等,在此不作详述。
4 频率测量的硬件实现及其测试
实际的测频装置因应用的时期、场合和要求不同,形式 各异。从早期的模拟、数字电路模块,到目前广泛使用单片机、工控机的内置程序信号处理,发展为通用或专用数字信号处理(DSP)应用于电力系统的状态估 计。实用的测频装置,一般经历了算法理论设计分析、仿真调试(稳态、动态和暂态)、程序固化和动模或实地实验等过程。
5 发展趋势
a.对电力系统频率本质认识的深入。
b.测频算法所基于的信号观测模型不断复杂化,以接近系统真实物理信号;求解方法从直观的函数解析,进入复杂的数值分析和数字信号处理领域。
c.硬件设备的精度、速度和可靠性的快速发展,为实现高性能算法和实时控制奠定了基础。
d.确定性、慢变频率偏移测量,转变为随机条件下快速动、暂态频率跟踪,这是电力系统安全稳定控制深入发展的需要。
e.频率估计与实时分析、控制目标相结合。
作者简介:谢小荣,男,1975年生,博士研究生,主要从事电力系统动态监控及FACTS方面的研究。
韩英铎,男,1938年生,教授,中国工程院院士,主要从事电力系统分析和控制、FACTS技术及GPS应用等领域的研究。
作者单位:清华大学电机工程系 100084 北京
参考文献
[1]Adamps R K, Mcintype J M, Symonds F W.
Characteristic of the Eastern Interconnection Line Frequency. IEEE Trans on
PWRS, 1982,101(12)
[2]闵 勇.复杂扩展式电力系统中功率—频率动态过程的分析及低频减载装置的整定:〔博士学位论文〕. 北京:清华大学, 1990
[3]Nguyen C T, Srinivasan K. A New Technique for
Rapid Tracking of Frequency Deviations Based on Level-Crossing. IEEE Trans on
PAS, 1984,103(8)
[4]胡艳婷,李本藩. 一种供安全自动装置用的新的频率测量算法. 电力系统自动化, 1987,11(6)
[5]Begovic M M, Djuric P M, Phadke A G.
Frequency Tracking in Power Networks in the Presence of Harmonics. IEEE Trans
on PWRD, 1993,8(2)
[6]索南加乐.一种不受电压过零点影响的新型频率测量方法. 西安交通大学学报,1995,29(3)
[7]何奔腾,李 菊.电力系统频率的自适应测量.电力系统及其自动化学报,1991,3(2)
[8]Sachdev M S, Wood H C, Johnson N. A Least
Error Square Technique for Determine Power System Frequency. IEEE Trans on
PAS,1985,104(2)
[9]Giray M M, Sachdev M S. Off-Nominal Frequency
Measurement in Electric Power System. IEEE Trans on PWRD, 1989,4(3)
[10]李振然. 利用递推最小二乘算法和自适应采样实现微机电量变送器. 电力系统自动化, 1995,19(3)
[11]Terzija V V, Djuric M B, Kovacevic B D. A New
Self-Tuning Algorithm for the Frequency Estimation of Distorted Signals. IEEE
Trans on PWRD, 1995,10(4)
[12]Soliman S A, Christensen G S, Kelly D H, et
al. An Algorithm for Frequency Relaying Based on Least Absolute Value
Approximation. Electric Power System Research, 1990,19(2)
[13]Djuric M B, Terzija V V. An Algorithm for
Frequency Relaying Based on the Newton-Raphson Method. Electric Power System
Research, 1994,31(2)
[14]Terzija V V, Djuric M B, Kovacevic B D, et
al. Voltage Phasor and System Frequency Estimation Using Newton-Type
Algorithm. IEEE Trans on PWRD, 1994, 9(3)
[15]Girgis A A, Daniel Hwang T L. Optimal
Estimation of Voltage Phasor and Frequency Deviation Using Linear and
Non-Linear Kalman Filtering: Theory and Limitation. IEEE Trans on PAS,
1984,103(10)
[16]Girgis A A, Peterson W L. Adaptive Estimation
of Power Frequency Deviation and Its Rate of Change for Calculating Sudden
Power System Overloads. IEEE Trans on PWRD, 1990,5(2)
[17]Sachdev M S, Wood H C, Johnson N. Kalman
Filtering Applied to Power System Measurement for Relaying. IEEE Trans on
PAS, 1984,103(2)
[18]Thorp J S, Phadke A G, Karmi K J. Real-Time
Voltage-Phasor Measurements for Static State Estimation. IEEE Trans on PAS,
1985,104(11)
[19]Girgis A A, Ham F M. A New FFT-Based Digital
Frequency Relay for Load Shedding. IEEE Trans on PAS, 1982,101(2)
[20]Phadek A G, Thorp J S, Adamiak M G. A New
Measurement Technique for Tracking Voltage Phasors, Local System Frequency,
and Rate of Change of Frequency. IEEE Trans on PAS, 1983, 102(5)
[21]丁仁杰.电力系统同步相量动态测量技术的研究与实现:〔博士学位论文〕.北京:清华大学电机系,1995
[22]Benmouyal Gabriel. An Adaptive
Sampling-Interval Generator for Digital Relaying. IEEE Trans on PWRD, 1989,
4(3)
[23]Hart David, Novosel Damir. A New Frequency
Tracking and Phasor Estimation Algorithm for Generator Protection. IEEE Trans
on PWRD, 1997, 12(3)
[24]Moore P J, Carran R D. Model System Tests on
a New Method of Power System Frequency Measurement. IEEE Trans on PWRD, 1996,
11(2)
[25]Moore P J, Allmeling J H, Johns A T.
Frequency Relaying Based on Instantaneous Frequency Measurement. IEEE Trans
on PWRD, 1996, 11(4)
[26]Akke Magnus. Frequency Estimation by
Demodulation of Two Complex Signals. IEEE Trans on PWRD, 1997, 12(1)
[27]Denys Ph, Ounan C, Hossenlopp L, et al.
Measurement of Voltage Phasors for the French Future Defense Against Losses
of Synchronism. IEEE Trans on PWRD, 1992,7(1)
[28]Eckhordt V, Hippe P, Hosmman G. Dynamic
Measuring of Frequency and Frequency Oscillations in Multiphase Power System.
IEEE Trans on PWRD, 1989, 4(1)
[29]Dowling E M, Ammann L P, Degroat R D. A
TQR-Iteration Based Adaptive SVD for Real Time Angle and Frequency Tracking.
IEEE Trans on Signal Processing, 1994, 42(4)
[30]Kezunovic M, Spasojevic P, Perunicic B. New
Digital Signal Processing Algorithm for Frequency Deviation Measurement. IEEE Trans on
PWRD, 1992, 7(3)
[31]韩英铎,王仲鸿,闵 勇,等.电力系统动态频率的定义及“虚拟转子法”频率相量研究.清华大学学报,1993,33(1)
1998-05-25收稿,1998-07-24改回。
|