MATLAB练习例子四(矩阵,Matrices)
返回
复数行列计算
》 z = [1+2i 3+4i; 4+5i 6+7i]
z =
1.0000 + 2.0000i 3.0000 + 4.0000i
4.0000 + 5.0000i 6.0000 + 7.0000i
》 inv(z)
ans =
-0.5833 + 0.5000i 0.3333 - 0.2500i
0.4167 - 0.3333i -0.1667 + 0.0833i
》 B = dlmread('ytest1.txt',';');
》 B
B =
1.0000 + 2.0000i 3.0000 + 4.0000i
5.0000 + 6.0000i 7.0000 + 8.0000i
》 inv(B)
ans =
-0.5000 + 0.4375i 0.2500 - 0.1875i
0.3750 - 0.3125i -0.1250 + 0.0625i
生成矩阵
n = input('Enter n ');
x = 1:n
J = [];
n = input('Enter n ');
lambda = input('Enter lambda ');
J = eye(n,n)*lambda;
for i = 1:n-1
J(i,i+1) = 1;
end
J
运行结果
Enter n 5
Enter lambda 0.33
J =
0.3300 1.0000 0 0 0
0 0.3300 1.0000 0 0
0 0 0.3300 1.0000 0
0 0 0 0.3300 1.0000
0 0 0 0 0.3300
Matrices in MATLAB
》 A = pascal(3)
A =
1 1 1
1 2 3
1 3 6
》 B = magic(3)
B =
8 1 6
3 5 7
4 9 2
》 C = fix(10*rand(3,2))
C =
9 4
2 8
6 7
》 U = [3; 1; 4]
U =
3
1
4
》 v = [2 0 -1]
v =
2 0 -1
》 s = 7
s =
7
》 X = A + B
X =
9 2 7
4 7 10
5 12 8
》 Y = X - A
Y =
8 1 6
3 5 7
4 9 2
》 X = A + C
??? エラー: ==> +
行列の次元は同じである必要があります.
》 W = v + s
W =
9 7 6
》 x = v*u
??? 'u' は未定義の関数、または変数です.
》 x = v*U
x =
2
》 X = U*v
X =
6 0 -3
2 0 -1
8 0 -4
》 X = B'
X =
8 3 4
1 5 9
6 7 2
》 x = v'
x =
2
0
-1
》 z = [1+2i 3+4i]
z =
1.0000 + 2.0000i 3.0000 + 4.0000i
》 z'
ans =
1.0000 - 2.0000i
3.0000 - 4.0000i
》
Matrix Multiplication
》 X = A*B
X =
15 15 15
26 38 26
41 70 39
》 Y = B*A
Y =
15 28 47
15 34 60
15 28 43
》 u = [3; 1; 4]
u =
3
1
4
》 x = A*u
x =
8
17
30
》 v = [2 0 -1]
v =
2 0 -1
》 y = v*B
y =
12 -7 10
》 C = fix(10*rand(3,2))
C =
9 4
2 8
6 7
》 X = A*C
X =
17 19
31 41
51 70
》 Y = C*A
??? エラー: ==> *
内部行列の次元は同じである必要があります.
》 s = 7
s =
7
》 w = s*v
w =
14 0 -7
Vector and Matrix Norms
》 [norm(v,1) norm(v) norm(v,inf)]
ans =
3.0000 2.2361 2.0000
》 [norm(C,1) norm(C) norm(C,inf)]
ans =
19.0000 14.8015 13.0000
行列的乘法和指数
》 A = pascal(3)
A =
1 1 1
1 2 3
1 3 6
》 X = A^2
X =
3 6 10
6 14 25
10 25 46
》 B = magic(3)
B =
8 1 6
3 5 7
4 9 2
》 Y = B^(-3)
Y =
0.0053 -0.0068 0.0018
-0.0034 0.0001 0.0036
-0.0016 0.0070 -0.0051
与行列的每个元素相乘
》 X = A.^2
X =
1 1 1
1 4 9
1 9 36
》 A = [0 -6 -1; 6 2 -16; -5 20 -10]
A =
0 -6 -1
6 2 -16
-5 20 -10
》 X0 = [1;1;1]
X0 =
1
1
1
》 X = [];
》 for t = 0:.01:1
X = [X expm(t*A)*x0];
end
??? 'x0' は未定義の関数、または変数です.
》 for t = 0:.01:1
X=[X expm(t*A)*X0];
end
》 plot3(X(1,:),X(2,:),X(3,:),'-o')
》 plot3(X(1,:),X(2,:),X(3,:),'-0')
??? Error in color/linetype argument
》 plot3(X(1,:),X(2,:),X(3,:),'-o')
》
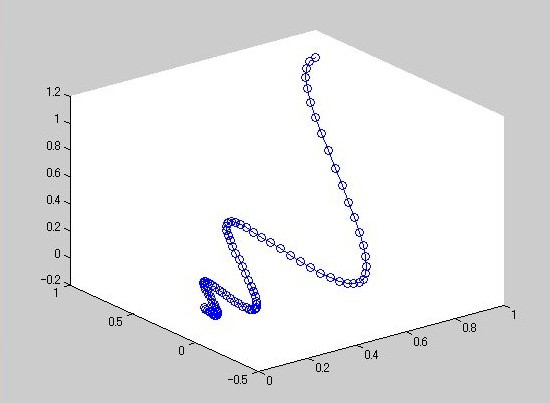
计算本征值(eigenvalue)
》 A = [ 0 -6 -1; 6 2 -16; -5 20 -10]
A =
0 -6 -1
6 2 -16
-5 20 -10
》 lambda = eig(A)
lambda =
-3.0710
-2.4645 +17.6008i
-2.4645 -17.6008i
》 [V,D] = eig(A)
V =
-0.8326 -0.1203 + 0.2123i -0.1203 - 0.2123i
-0.3553 0.4691 + 0.4901i 0.4691 - 0.4901i
-0.4248 0.6249 - 0.2997i 0.6249 + 0.2997i
D =
-3.0710 0 0
0 -2.4645 +17.6008i 0
0 0 -2.4645 -17.6008i
缺陷行列(defective matrices)
》 A = [6 12 19; -9 -20 -33; 4 9 15]
A =
6 12 19
-9 -20 -33
4 9 15
》 [V,D] = eig(A)
V =
0.4741 0.4082 -0.4082
-0.8127 -0.8165 0.8165
0.3386 0.4082 -0.4082
D =
-1.0000 0 0
0 1.0000 0
0 0 1.0000
》 [X,J] = jordan(A)
??? 'jordan' は未定義の関数、または変数です.
Schur decomposition
》 [U,S] = schur(A)
U =
0.4741 -0.6571 0.5861
-0.8127 -0.0706 0.5783
0.3386 0.7505 0.5675
S =
-1.0000 21.3737 44.4161
0 1.0081 0.6095
0 -0.0001 0.9919
》
奇异值分解
》 A = [9 4; 6 8; 2 7]
A =
9 4
6 8
2 7
》 [U,S,V] = svd(A)
U =
0.6105 -0.7174 0.3355
0.6646 0.2336 -0.7098
0.4308 0.6563 0.6194
S =
14.9359 0
0 5.1883
0 0
V =
0.6925 -0.7214
0.7214 0.6925
》 [U,S,V] = svd(A,0)
U =
0.6105 -0.7174
0.6646 0.2336
0.4308 0.6563
S =
14.9359 0
0 5.1883
V =
0.6925 -0.7214
0.7214 0.6925
》
返回
